矩阵的三角分解

矩阵的三角分解就是从高斯消去法得到的，针对不同类型的矩阵，通过改变矩阵分解的方式，可以减少一定的计算量。这一块其实如果应付考试的话，只需要掌握矩阵的LU分解，在矩阵为对称正定情况下的平方根法和改进平方根法，与三对角情况下的追赶法。

矩阵的LU分解

从之前的高斯消去法中我们可以发现，对方程组进行变换消元时，等价于矩阵左乘初等矩阵

在实际问题中，经常遇到系数矩阵$A$相同，但右端项不同的多个线性方程组$Ax=b^{(i)}(i=1,2,\cdots,m)$. 对高斯消去法作进一步的输入分析，由矩阵运算到处矩阵的三角分解法。利用矩阵的三角分解求解上述的一类线性方程组，以达到减少运算量的目的。其次，针对具有特殊系数矩阵的线性方程组，由矩阵的三角分解建立一些特殊的求解方法。

从矩阵运算的观点来看，高斯消去法的消元过程实质上是将增广矩阵$(A^{(0)},b^{(0)})$通过逐步左乘一些列的初等下三角矩阵$L_k(k=1,2,\cdots,n-1)$最终变为矩阵$(A^{(n-1)},b^{(n-1)})$.

一般地，
$$
\begin{aligned}
&A^{(k-1)} \triangleq\left(\begin{array}{ccccc}
a_{11}^{(0)} & a_{12}^{(0)} & & \ldots & \cdots & a_{1 n}^{(0)} \\
& a_{22}^{(1)} & & \cdots & \cdots & a_{2 n}^{(1)} \\
& & \ddots & & & \vdots \\
& & & a_{k k}^{(k-1)} & \cdots & a_{k n}^{(k-1)} \\
& & & \vdots & & \vdots\\
& & & a_{n k}^{(k-1)} & \cdots & a_{n n}^{(k-1)}
\end{array}\right)\\
&\qquad L_{k} \triangleq\left(\begin{array}{ccccccc}
1 & & & & & & \\
& \ddots & & & & & \\
& & 1 & & & & \\
& & -l_{k+1, k} & 1 & & \\
& & -l_{k+2, k} & & 1 & \\
& & \vdots & & & \ddots \\
& & -l_{n k} & & & & 1
\end{array}\right)\\
&\quad A^{(k)} \triangleq\left(\begin{array}{cccccc}
a_{11}^{(0)} & a_{12}^{(0)} & & \ldots & a_{1, k+1}^{(0)} & \cdots & a_{1 n}^{(0)} \\
& a_{22}^{(1)} & & \cdots & a_{2, k+1}^{(1)} & \cdots & a_{2 n}^{(1)} \\
& & \ddots & & \vdots & & \vdots \\
& & & a_{k k}^{(k-1)} & a_{k, k+1}^{(k-1)} & \cdots & a_{k n}^{(k-1)} \\
& & & & a_{k+1, k+1}^{(k)} & \cdots & a_{k+1, n}^{(k)} \\
& & & & \vdots & & \vdots \\
& & & & a_{n, k+1}^{(k)} & \cdots & a_{n n}^{(k)}
\end{array}\right)
\end{aligned}
$$

则$A^{(k)}=L_{k} A^{(k-1)}=L_{k} L_{k-1} \cdots L_{2} L_{1} A^{(0)}$ 故若高斯消去法能顺利进行下去，则线性方程组的系数矩阵$A$可以分解成一个单位下三角矩阵$L$与一个上三角矩阵$U$的乘积，且唯一，即
$$
A=LU
$$
其中
$$
\begin{array}{c}
A=\left(\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1 n} \\
a_{21} & a_{22} & \cdots & a_{2 n} \\
\vdots & \vdots & & \vdots \\
a_{n 1} & a_{n 2} & \cdots & a_{n n}
\end{array}\right), \quad L=\left(\begin{array}{ccccc}
1 & & \\
l_{21} & 1 & & \\
\vdots & \vdots & & \ddots & \\
l_{n 1} & l_{n 2} & \cdots & l_{n, n-1} & 1
\end{array}\right) \\
U=\left(\begin{array}{cccc}
u_{11} & u_{12} & \cdots & u_{1 n} \\
& u_{22} & \cdots & u_{2 n} \\
& & \ddots & \vdots \\
& & & u_{n n}
\end{array}\right) .
\end{array}
$$

根据推导，$A=LU$分解公式如下
$$
\left\{\begin{array}{ll}
u_{1 j}=a_{1 j}, & j=1,2, \cdots, n \\
l_{i 1}=\frac{a_{i 1}}{u_{11}}, & i=2,3, \cdots, n \\
u_{i j}=a_{i j}-\sum_{k=1}^{i-1} l_{i k} u_{k j}, & i=2,3, \cdots, n ; j=i, i+1, \cdots, n \\
a_{i j}-\sum_{k=1}^{j-1} l_{i k} u_{k j} & \\
l_{i j}=\frac{a_{i j}-\sum_{k=1}^{j-1} l_{i k} u_{k j}}{u_{j j}}, & j=2,3, \cdots, n-1 ; i=j+1, j+2, \cdots, n
\end{array}\right.
$$
上面介绍的将矩阵分解为单位下三角$L$和上三角矩阵$U$ 的乘积称为杜立特分解(Doolittle)，同理也有将矩阵分解成单位上三角和下三角矩阵乘积的方法，称为克劳特（Crout）分解，实际手工运算时常常采用LU分解的紧凑格式，具体如下，那招先横后竖依次计算
$$
\begin{array}{lcccc}
u_{11} & u_{12} & u_{13} & \cdots & u_{1 n} \\
l_{21} & u_{22} & u_{23} & \cdots & u_{2 n} \\
l_{31} & l_{32} & u_{33} & \cdots & u_{3 n} \\
l_{41} & l_{42} & l_{43} & & \\
\vdots & \vdots & \vdots & & \\
l_{n 1} & l_{n 2} & l_{n 3} & & u_{n n}
\end{array}
$$
以例题辅助紧凑格式的说明

矩阵分解的平方根法和改进平方法

平方根法

在用有限元法求解结构力学和最优化方法等诸多问题中，都需要求解一个系数矩阵时对称矩阵的线性方程$Ax=b$针对这种方程组的特点，有一种叫LU分解更为有效的求解方法——平方根法，所谓平方根法，就是将矩阵$A$分解为成一个下三角矩阵和该下三角矩阵的转置的乘积，然后利用这种分解求解线性方程组$Ax=b$.这种分解也成为对称正定矩阵的楚列斯基（Cholesky）分解，即
$$
A=GG^{\rm T}
$$
由证明可得（搞工程的要啥证明），该分解在矩阵为对称正定矩阵时是可以分解进行下去的，分解公式如下
记
$$
G \triangleq\left(\begin{array}{ccccc}
g_{11} & & & & \\
g_{21} & g_{22} & & & \\
g_{31} & g_{32} & g_{33} & & \\
\vdots & \vdots & & \ddots & \\
g_{n 1} & g_{n 2} & \cdots & g_{n, n-1} & g_{n n}
\end{array}\right)\\
$$
则
$$\left\{\begin{aligned}
g_{11} &=\sqrt{a_{11}} \\
g_{i 1} &=\frac{a_{i 1}}{g_{11}}, \\
g_{j j} &=\left(a_{j j}-\sum_{k=1}^{j-1} g_{j k}^{2}\right)^{\frac{1}{2}}, \quad j=2,3, \cdots, n \\
g_{i j} &=\frac{a_{i j}-\sum_{k=1}^{j-1} g_{i k} g_{j k}}{g_{j j}}, \quad j=2,3, \cdots, n-1 ; i=j+1, j+2, \cdots, n
\end{aligned}\right.
$$
同样的，平方根法在手工计算时也有紧凑格式如下
$$
\begin{array}{cccccc}
g_{11} & g_{21} & g_{31} & \cdots & g_{n 1} & y_{1} \\
g_{21} & g_{22} & g_{32} & \cdots & g_{n 2} & y_{2} \\
g_{31} & g_{32} & g_{33} & \cdots & g_{n 3} & y_{3} \\
\vdots & \vdots & \vdots & \ddots & & \\
g_{n 1} & g_{n 2} & g_{n 3} & & g_{n n} & y_{n}
\end{array}
$$
使用平方根法对上道例题进行求解介绍

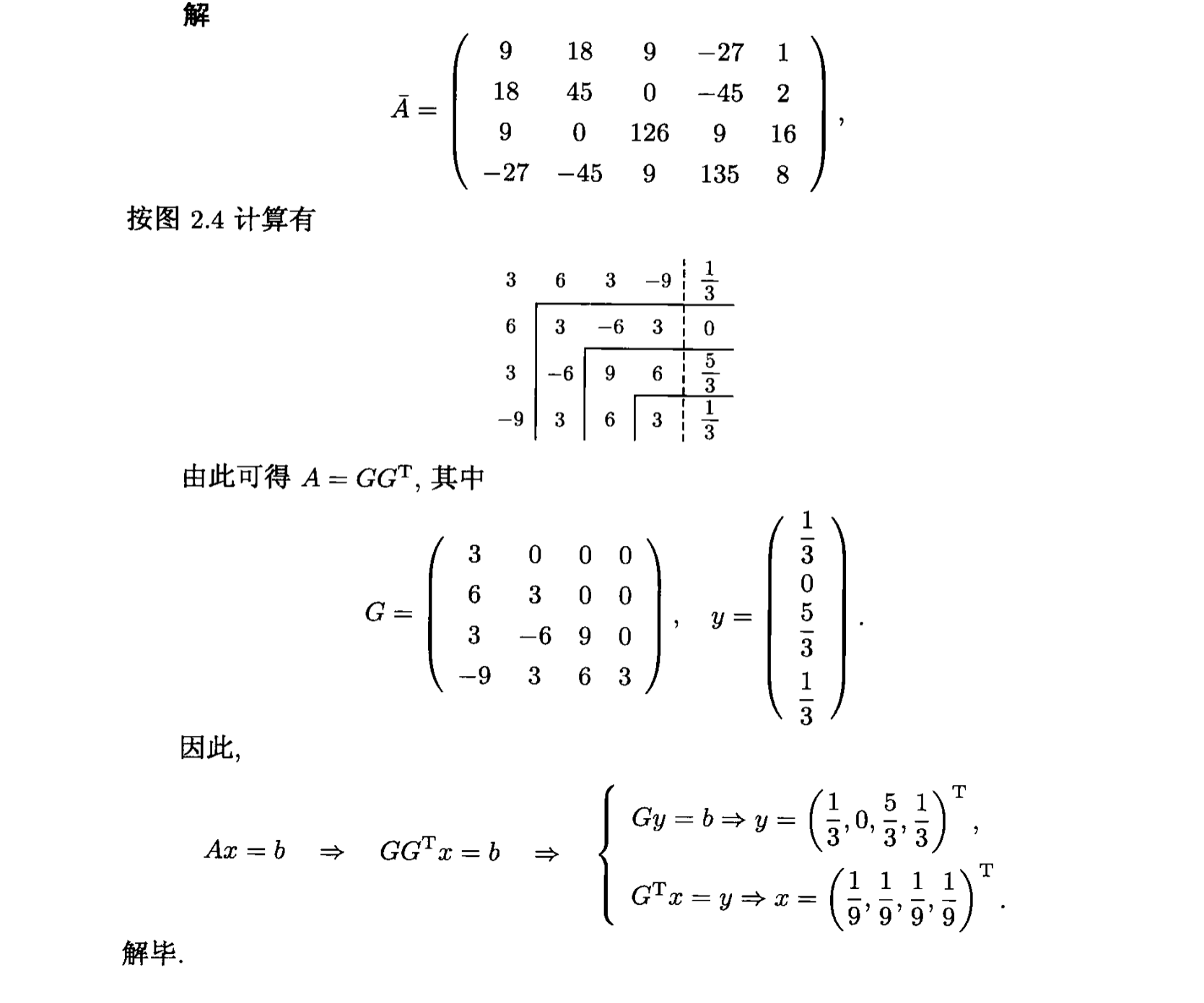
改进的平方根法

平方根法相较于高斯消去法和杜立特分解减少了近一般的运算量，但是求解释需要进行开方运算，需要消耗较多的机器时间，为避免平方根法的开方运算，对矩阵$A$进行$A=LDL^{\rm T}$（搞工程要啥证明，梅开二度），称为改进的平方根法，分解公式如下
$$
\left\{\begin{array}{ll}
u_{i j}=a_{i j}-\sum_{k=1}^{i-1} l_{i k} u_{k j}, & i=1,2, \cdots, n ; j=i, i+1, \cdots, n \\
l_{j i}=\frac{u_{i j}}{u_{i i}}, & i=1,2, \cdots, n-1 ; j=i+1, i+2, \cdots, n
\end{array}\right.
$$

具体计算公式如下
$$
A x=b \quad \Rightarrow \quad L D L^{\mathrm{T}} x=b \quad \Rightarrow\left\{\begin{array}{l}
L y=b \Rightarrow \text { 解出 } y, \\
D z=y \Rightarrow \text { 解出 } z, \\
L^{\mathrm{T}} x=z \Rightarrow \text { 解出 } x .
\end{array}\right.
$$
由$Ly=b$得
$$
y_1=b_1\\
y_i=b_i-\sum_{k=1}^{i-1}l_{ki}y_k,\quad i=2,3,\cdots,n
$$
由$Dz=y$得
$$
z_i=\frac{y_i}{u_{ii}},\quad i=1,2,\cdots,n.
$$
由$L^{\rm T}x=z$得
$$
\left\{\begin{array}{l}
x_{n}=z_{n} \\
x_{i}=z_{i}-\sum_{k=i+1}^{n} l_{k i} x_{k}, \quad i=n-1, n-2, \cdots, 2,1
\end{array}\right.
$$
其实公式乱七八糟，本质上还是LU分解，将U的对角线元素作为D，将原矩阵拆分成三个矩阵，求解三个方程即可

追赶法

在样条插值函数、常微分方程边值问题和热传导方程的有限差分法等问题中，常遇到求解三对角方程组$Ax=d$,即
$$
\left(\begin{array}{ccccc}
b_{1} & c_{1} & & & \\
a_{2} & b_{2} & c_{2} & & \\
& \ddots & \ddots & \ddots & \\
& & a_{n-1} & b_{n-1} & c_{n-1} \\
& & & a_{n} & b_{n}
\end{array}\right)\left(\begin{array}{c}
x_{1} \\
x_{2} \\
\vdots \\
x_{n-1} \\
x_{n}
\end{array}\right)=\left(\begin{array}{c}
d_{1} \\
d_{2} \\
\vdots \\
d_{n-1} \\
d_{n}
\end{array}\right)
$$
通常$A$是严格对角占优矩阵，严格对角占优矩阵存在唯一的杜立特分解，对于三对角矩阵，有如下形式的杜立特分解
$$
A=L U=\left(\begin{array}{ccccc}
1 & & & & \\
l_{2} & 1 & & & \\
& \ddots & \ddots & & \\
& & l_{n-1} & 1 & \\
& & & l_{n} & 1
\end{array}\right)\left(\begin{array}{ccccc}
u_{1} & c_{1} & & & \\
& u_{2} & c_{2} & & \\
& & \ddots & \ddots & \\
& & & u_{n-1} & c_{n-1} \\
& & & & u_{n}
\end{array}\right)
$$
根据矩阵乘法易得
$$
\left\{\begin{array}{ll}
u_{1}=b_{1}, & \\
l_{i}=\frac{a_{i}}{u_{i-1}}, & i=2,3, \cdots, n, \\
u_{i}=b_{i}-l_{i} c_{i-1}, & i=2,3, \cdots, n .
\end{array}\right.
$$
用LU分解三对角矩阵求解称为追赶法，追赶法的乘除法运算次数仅为$5n-4$，比高斯消去法的运算次数少得多，不过本质上还是LU分解就是了，例题如下