2. 时域性能指标的计算

2.1 系统的时域指标

2.1.1 一阶系统的时间响应

时间常数T
上升时间T~r~(时间响应曲线从终值的0.1到0.9的时间)
过渡时间T~s~（时间响应曲线响应值与终值相比，误差稳定在2%以内的时间）

2.1.2 二阶系统的时间响应

延迟时间T~d~（单位阶跃响应第一次超过稳态值达到峰值所需的时间）
上升时间T~r~（欠阻尼系统单位阶跃响应第一次从0上升到稳态值的100%所需时间；过阻尼系统单位阶跃响应第一次从稳态值10%上升到90%所需的时间）
峰值时间T~p~（单位阶跃响应第一次超过稳态值达到峰值所需时间）
相对超调量%OS （响应曲线在峰值时刻，响应值超出稳态值的量值，表征为稳态值的百分数）
调整时间T~s~ （单位阶跃响应与稳态值之差，进入允许的误差范围所需时间）

2.2 系统构建

函数	备注
`ss(A,B,C,D[,dt])`	通过状态方程构建控制系统
`tf(num,den[,dt])`	通过传递函数构建控制系统

2.2.1 control.ss

control.ss(A,B,C,D[,dt]) 通过状态方程来描述系统

该函数接收1，4或5个参数输入：

ss(sys) ：将线性系统A转换为状态方程；
ss(A, B, C, D)：函数接收系统矩阵A，控制矩阵B，输出矩阵C，和反馈矩阵D构建状态空间系统；

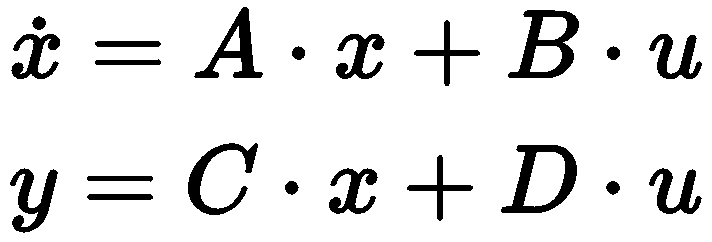
ss(A, B, C, D, dt)：同上函数接收系统矩阵A，控制矩阵B，输出矩阵C，和D构建离散的状态空间系统。

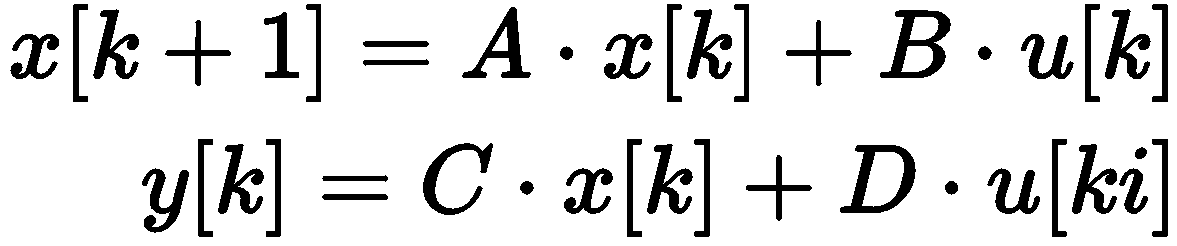
2.2.2 control.tf

control.tf(num,den[,dt]) 通过传递函数来描述系统，同时也可描述多输入多输出系统

该函数接收1，2或3个参数输入：

tf(sys)：将一线性系统转换为传递函数形式，该方法总是会输出一个新系统；

tf(num, den) ：通过分子（num）和分母（den）的多项式系数来创建系统的传递函数；

tf(num, den, dt)：通过分子（num）和分母（den）的多项式系数来创建一个离散系统的传递函数。

2.3 系统的时域分析

方法	备注
`step(sys[, T, X0, input, output, return_x])`	线性系统的单位阶跃响应（中括号中参数可选，下同）
`impulse(sys[, T, X0, input, output, return_x])`	线性系统的单位脉冲响应
`initial(sys[, T, X0, input, output, return_x])`	线性系统的零状态响应
`stepinfo(sysdata, T, yfinal, SettlingTimeThreshold, RiseTimeLimits)`	输出系统系统阶跃响应的性能指标

2.3.1 control.matlab.step

三个函数输入与输出参数类型相同，以下仅以step 为例：

control.matlab.step(sys, T=None, X0=0.0, input=0, output=None, return_x=False)

输入值

sys(StateSpace, or TransferFunction) - 欲分析的线性时不变系统，输入数据类型为状态方程或传递函数；
T(arry-like or number, optional) - 可选参数，数据类型为时间向量或者模拟持续时间；
X0(arry-like or number, optional) - 可选参数，系统的初始状态，默认为零；
input(int) - 标识多输入多输出系统中的输入；
output(int) - 标识多输入多输出系统中的输出。

输出值

yout(array) - 以列表形式返回系统的响应；
T(arry) - 列表的形式返回输出的时间值；
xout(array(if selected)) - 每个x变量的单独响应。

2.3.2 control.matlab.stepinfo

stepinfo(sysdata, T=None, yfinal=None, SettlingTimeThreshold, RiseTimeLimits)

输入值

sysdata - 线性定常系统的状态方程或传递函数，或者单位阶跃响应的时间序列；
T - 可选参数，系统单位阶跃响应持续时间；
yfinal - 可选参数，系统的稳态响应；
SettlingTimeThreshold - 可选参数，计算过渡时间的误差，默认为0.02；
RiseTimeLimits - 定义上升时间的上下限，默认为(0.1, 0.9)

输出值

对于单输入单输出系统，stepinfo 返回一个字典，包含以下部分：

RiseTime - 第一次从稳态值的10%上升到90%的时间；
SettlingTime - 系统调整时间；
SettlingMin - 上升时间后输出最小值；
SettingMax - 上升时间后输出最大值；
Overshoot - 系统超调量；
UnderShoot - 系统下冲量；
Peak - 系统峰值；
PeakTime - 系统峰值时间。

输出字典示例：

{'RiseTime': 1.6746073403593051, 'SettlingTime': 8.093935478403308, 'SettlingMin': 0.9394891622475169, 'SettlingMax': 1.1630334929041959, 'Overshoot': 16.30334929041959, 'Undershoot': 0, 'Peak': 1.1630334929041959, 'PeakTime': 3.628315904111828, 'SteadyStateValue': 1.0}

2.3.3 示例

求二阶欠阻尼系统阶跃响应：

# second.py - 二阶欠阻尼系统单位阶跃响应

import os
import matplotlib.pyplot as plt  # MATLAB 作图函数
from control.matlab import *  # MATLAB类函数

# 系统参数设置
m = 250.0  # 系统质量
k = 40.0  # 弹簧刚度系数
b = 60.0  # 阻尼系数

# 系统矩阵
A = [[0, 1.], [-k / m, -b / m]]
B = [[0], [1 / m]]
C = [[1., 0]]
sys = ss(A, B, C, 0)

# Step response for the system
plt.figure(1)
yout, T = step(sys)
plt.plot(T.T, yout.T)
plt.show(block=False)

# 系统Bode图
plt.figure(2)
mag, phase, om = bode(sys, logspace(-2, 2), plot=True)
plt.show(block=False)

# 系统Nyquist图
plt.figure(3)
nyquist(sys)
plt.show(block=False)

# 系统根轨迹
rlocus(sys)

if &#039;PYCONTROL_TEST_EXAMPLES&#039; not in os.environ:
    plt.show()

绘制二阶系统单位阶跃响应：

# step_response.py - 绘制二阶系统单位阶跃响应并输出调整时间
import os
import matplotlib.pyplot as plt  # MATLAB plotting functions
from control.matlab import *  # MATLAB-like functions

# 二阶欠阻尼系统参数
wn = 1  # 系统固有频率
ksi = 0.5  # 系统阻尼

sys = tf(wn ** 2, [1, 2 * ksi * wn, wn ** 2]) #通过传函表示系统

# 绘制系统单位阶跃响应图
plt.figure(1)
yout, T = step(sys)
plt.plot(T.T, yout.T)
plt.show(block=False)

# 获取系统单位阶跃响应的调整时间
S = stepinfo(sys)
print("调节时间:", S[&#039;SettlingTime&#039;])